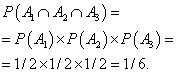Необходимость в действиях над вероятностями наступает тогда, когда известны вероятности некоторых событий, а вычислить нужно вероятности других событий, которые связаны с данными событиями.
Сложение вероятностей используется тогда, когда нужно вычислить вероятность объединения или логической суммы случайных событий.
Сумму событий A
и B
обозначают A
+ B
или
A
∪ B
. Суммой двух событий называется событие, которое наступает тогда и только тогда, когда наступает хотя бы одно из событий. Это означает, что A
+ B
– событие, которое наступает тогда и только тогда, когда при наблюдении произошло событие A
или событие B
, или одновременно A
и B
.
Если события A
и B
взаимно несовместны и их вероятности даны, то вероятность того, что в результате одного испытания произойдёт одно из этих событий, рассчитывают, используя сложение вероятностей.
Теорема сложения вероятностей.
Вероятность того, что произойдёт одно из двух взаимно несовместных событий, равна сумме вероятностей этих событий:
Например, на охоте произведены два выстрела. Событие А
– попадание в утку с первого выстрела, событие В
– попадание со второго выстрела, событие (А
+ В
) – попадание с первого или второго выстрела или с двух выстрелов. Итак, если два события А
и В
– несовместные события, то А
+ В
– наступление хотя бы одного из этих событий или двух событий.
Пример 1.
В ящике 30 мячиков одинаковых размеров: 10 красных, 5 синих и 15 белых. Вычислить вероятность того, что не глядя будет взят цветной (не белый) мячик.
Решение. Примем, что событие А
– «взят красный мячик», а событие В
– «взят синий мячик». Тогда событие – «взят цветной (не белый) мячик». Найдём вероятность события А
:
и события В
:
События А
и В
– взаимно несовместные, так как если взят один мячик, то нельзя взять мячики разных цветов. Поэтому используем сложение вероятностей:
Теорема сложения вероятностей для нескольких несовместных событий.
Если события составляют полное множество событий, то сумма их вероятностей равна 1:
Сумма вероятностей противоположных событий также равна 1:
Противоположные события образуют полное множество событий, а вероятность полного множества событий равна 1.
Вероятности противоположных событий обычно обозначают малыми буквами p
и q
. В частности,
из чего следуют следующие формулы вероятности противоположных событий:
Пример 2.
Цель в тире разделена на 3 зоны. Вероятность того что некий стрелок выстрелит в цель в первой зоне равна 0,15, во второй зоне – 0,23, в третьей зоне – 0,17. Найти вероятность того, что стрелок попадет в цель и вероятность того, что стрелок попадёт мимо цели.
Решение: Найдём вероятность того, что стрелок попадёт в цель:
Найдём вероятность того, что стрелок попадёт мимо цели:
Задачи посложнее, в которых нужно применять и сложение и умножение вероятностей –
на странице “Различные задачи на сложение и умножение вероятностей” .
Сложение вероятностей взаимно совместных событий
Два случайных события называются совместными, если наступление одного события не исключает наступления второго события в том же самом наблюдении. Например, при бросании игральной кости событием А
считается выпадение числа 4, а событием В
– выпадение чётного числа. Поскольку число 4 является чётным числом, эти два события совместимы. В практике встречаются задачи по расчёту вероятностей наступления одного из взаимно совместных событий.
Теорема сложения вероятностей для совместных событий.
Вероятность того, что наступит одно из совместных событий, равна сумме вероятностей этих событий, из которой вычтена вероятность общего наступления обоих событий, то есть произведение вероятностей.
Формула вероятностей совместных событий имеет следующий вид:
Поскольку события А
и В
совместимы, событие А
+ В
наступает, если наступает одно из трёх возможных событий: или АВ
. Согласно теореме сложения несовместных событий,
вычисляем так:
Событие А
наступит, если наступит одно из двух несовместных событий: или АВ
. Однако вероятность наступления одного события из нескольких несовместных событий равна сумме вероятностей всех этих событий:
Читайте также:
Аналогично:
Подставляя выражения (6) и (7) в выражение (5), получаем формулу вероятности для совместных событий:
При использовании формулы (8) следует учитывать, что события А
и В
могут быть:
- взаимно независимыми;
- взаимно зависимыми.
Формула вероятности для взаимно независимых событий:
Формула вероятности для взаимно зависимых событий:
Если события А
и В
несовместны, то их совпадение является невозможным случаем и, таким образом, P
(AB
) = 0. Четвёртая формула вероятности для несовместных событий такова:
Пример 3.
На автогонках при заезде на первой автомашине вероятность победить , при заезде на второй автомашине . Найти:
- вероятность того, что победят обе автомашины;
- вероятность того, что победит хотя бы одна автомашина;
1) Вероятность того, что победит первая автомашина, не зависит от результата второй автомашины, поэтому события А
(победит первая автомашина) и В
(победит вторая автомашина) – независимые события. Найдём вероятность того, что победят обе машины:
2) Найдём вероятность того, что победит одна из двух автомашин:
Задачи посложнее, в которых нужно применять и сложение и умножение вероятностей –
на странице “Различные задачи на сложение и умножение вероятностей” .
Решить задачу на сложение вероятностей самостоятельно, а затем посмотреть решение
Пример 4.
Бросаются две монеты.
Событие A
– выпадение герба на первой монете.
Событие B– выпадение герба на второй монете.
Найти вероятность события C = A
+ B
.
Умножение вероятностей
Умножение вероятностей используют, когда следует вычислить вероятность логического произведения событий.
При этом случайные события должны быть независимыми. Два события называются взаимно независимыми, если наступление одного события не влияет на вероятность наступления второго события.
Теорема умножения вероятностей для независимых событий.
Вероятность одновременного наступления двух независимых событий А
и В
равна произведению вероятностей этих событий и вычисляется по формуле:
Пример 5.
Монету бросают три раза подряд. Найти вероятность того, что все три раза выпадет герб.
Решение. Вероятность того, что при первом бросании монеты выпадет герб , во второй раз , в третий раз . Найдём вероятность того, что все три раза выпадет герб:
Решить задачи на умножение вероятностей самостоятельно, а затем посмотреть решение
Пример 6.
Имеется коробка с девятью новыми теннисными мячами.
Для игры берут три мяча, после игры их кладут обратно. При выборе мячей игранные от неигранных не
отличают. Какова вероятность того, что после трёх игр в коробке не останется неигранных мячей?
Пример 7.
32 буквы русского алфавита написаны на карточках
разрезной азбуки. Пять карточек вынимаются наугад одна за другой и укладываются на стол в порядке
появления. Найти вероятность того, что из букв получится слово “конец”.
Пример 8.
Из полной колоды карт (52 листа) вынимаются сразу
четыре карты. Найти вероятность того, что все эти четыре карты будут разных мастей.
Пример 9.
Та же задача, что в примере 8, но каждая карта
после вынимания возвращается в колоду.
Задачи посложнее, в которых нужно применять и сложение и умножение вероятностей, а
также вычислять произведение нескольких событий –
на странице “Различные задачи на сложение и умножение вероятностей” .
Вероятность того, что произойдёт хотя бы одно из взаимно независимых событий , можно вычислить путём вычитания из 1 произведения вероятностей противоположных событий , то есть по формуле:
Пример 10.
Грузы доставляют тремя видами транспорта: речным, железнодорожным и автотранспортом. Вероятность того, что груз будет доставлен речным транспортом, составляет 0,82, железнодорожным транспортом 0,87, автотранспортом 0,90. Найти вероятность того, что груз будет доставлен хотя бы одним из трёх видов транспорта.
Начальный уровень
Что такое вероятность?
Столкнувшись с этим термином первый раз, я бы не понял, что это такое. Поэтому попытаюсь объяснить доступно.
Вероятность – это шанс того, что произойдет нужное нам событие.
Например, ты решил зайти к знакомому, помнишь подъезд и даже этаж на котором он живет. А вот номер и расположение квартиры забыл. И вот стоишь ты на лестничной клетке, а перед тобой двери на выбор.
Каков шанс (вероятность) того, что если ты позвонишь в первую дверь, тебе откроет твой друг? Всего квартиры, а друг живет только за одной из них. С равным шансом мы можем выбрать любую дверь.
Но каков этот шанс?
Дверей, нужная дверь. Вероятность угадать, позвонив в первую дверь: . То есть один раз из трех ты точно угадаешь.
Мы хотим узнать, позвонив раз, как часто мы будем угадывать дверь? Давай рассмотри все варианты:
- Ты позвонил в 1ю
дверь - Ты позвонил в 2ю
дверь - Ты позвонил в 3ю
дверь
А теперь рассмотрим все варианты, где может находиться друг:
а. За 1ой
дверью
б. За 2ой
дверью
в. За 3ей
дверью
Сопоставим все варианты в виде таблицы. Галочкой обозначены варианты, когда твой выбор совпадает с местоположением друга, крестиком – когда не совпадает.
Как видишь всего возможно
вариантов
местоположения друга и твоего выбора, в какую дверь звонить.
А благоприятных исходов всего
.
То есть раза из ты угадаешь, позвонив в дверь раз, т.е. .
Это и есть вероятность – отношение благоприятного исхода (когда твой выбор совпал с местоположение друга) к количеству возможных событий.
Определение – это и есть формула. Вероятность принято обозначать p, поэтому:
Такую формулу писать не очень удобно, поэтому примем за – количество благоприятных исходов, а за – общее количество исходов.
Вероятность можно записывать в процентах, для этого нужно умножить получившийся результат на:
Наверное, тебе бросилось в глаза слово «исходы». Поскольку математики называют различные действия (у нас такое действие – это звонок в дверь) экспериментами, то результатом таких экспериментов принято называть исход.
Ну а исходы бывают благоприятные и неблагоприятные.
Давай вернемся к нашему примеру. Допустим, мы позвонили в одну из дверей, но нам открыл незнакомый человек. Мы не угадали. Какова вероятность, что если позвоним в одну из оставшихся дверей, нам откроет наш друг?
Если ты подумал, что, то это ошибка. Давай разбираться.
У нас осталось две двери. Таким образом, у нас есть возможные шаги:
1) Позвонить в 1-ую
дверь
2) Позвонить во 2-ую
дверь
Друг, при всем этом, точно находится за одной из них (ведь за той, в которую мы звонили, его не оказалось):
а) Друг за 1-ой
дверью
б) Друг за 2-ой
дверью
Давай снова нарисуем таблицу:
Как видишь, всего есть варианта, из которых – благоприятны. То есть вероятность равна.
А почему не?
Рассмотренная нами ситуация – пример зависимых событий.
Первое событие – это первый звонок в дверь, второе событие – это второй звонок в дверь.
А зависимыми они называются потому что влияют на следующие действия. Ведь если бы после первого звонка в дверь нам открыл друг, то какова была бы вероятность того, что он находится за одной из двух других? Правильно, .
Но если есть зависимые события, то должны быть и независимые
? Верно, бывают.
Хрестоматийный пример – бросание монетки.
- Бросаем монетку раз. Какова вероятность того, что выпадет, например, орел? Правильно – , ведь вариантов всего (либо орел, либо решка, пренебрежем вероятностью монетки встать на ребро), а устраивает нас только.
- Но выпала решка. Ладно, бросаем еще раз. Какова сейчас вероятность выпадения орла? Ничего не изменилось, все так же. Сколько вариантов? Два. А сколько нас устраивает? Один.
И пусть хоть тысячу раз подряд будет выпадать решка. Вероятность выпадения орла на раз будет все также. Вариантов всегда, а благоприятных – .
Отличить зависимые события от независимых легко:
- Если эксперимент проводится раз (раз бросают монетку, 1 раз звонят в дверь и т.д.), то события всегда независимые.
- Если эксперимент проводится несколько раз (монетку бросают раз, в дверь звонят несколько раз), то первое событие всегда независимое. А дальше, если количество благоприятных или количество всех исходов меняется, то события зависимые, а если нет – независимые.
Давай немного потренируемся определять вероятность.
Пример 1.
Монетку бросают два раза. Какова вероятность того, что два раза подряд выпадет орел?
Решение:
Рассмотрим все возможные варианты:
- Орел-орел
- Орел-решка
- Решка-орел
- Решка-решка
Как видишь, всего варианта. Из них нас устраивает только. То есть вероятность:
Если в условии просят просто найти вероятность, то ответ нужно давать в виде десятичной дроби. Если было бы указано, что ответ нужно дать в процентах, тогда мы умножили бы на.
Ответ:
Пример 2.
В коробке конфет все конфеты упакованы в одинаковую обертку. Однако из конфет – с орехами, с коньяком, с вишней, с карамелью и с нугой.
Какова вероятность, взяв одну конфету, достать конфету с орехами. Ответ дайте в процентах.
Решение:
Сколько всего возможных исходов? .
То есть, взяв одну конфету, она будет одной из, имеющихся в коробке.
А сколько благоприятных исходов?
Потому что в коробке только конфет с орехами.
Ответ:
Пример 3.
В коробке шаров. из них белые, – черные.
- Какова вероятность вытащить белый шар?
- Мы добавили в коробку еще черных шаров. Какова теперь вероятность вытащить белый шар?
Решение:
а) В коробке всего шаров. Из них белых.
Вероятность равна:
б) Теперь шаров в коробке стало. А белых осталось столько же – .
Ответ:
Полная вероятность
| Вероятность всех возможных событий равна (). |
Допустим, в ящике красных и зеленых шаров. Какова вероятность вытащить красный шар? Зеленый шар? Красный или зеленый шар?
Вероятность вытащить красный шар
Зеленый шар:
Красный или зеленый шар:
Как видишь, сумма всех возможных событий равна (). Понимание этого момента поможет тебе решить многие задачи.
Пример 4.
В ящике лежит фломастеров: зеленых, красных, синих, желтых, черный.
Какова вероятность вытащить НЕ красный фломастер?
Решение:
Давай посчитаем количество благоприятных исходов.
НЕ красный фломастер, это значит зеленый, синий, желтый или черный.
Вероятность всех событий. А вероятность событий, которые мы считаем неблагоприятными (когда вытащим красный фломастер) – .
Таким образом, вероятность вытащить НЕ красный фломастер – .
Ответ:
| Вероятность того, что событие не произойдет, равна минус вероятность того, что событие произойдет. |
Правило умножения вероятностей независимых событий
Что такое независимые события ты уже знаешь.
А если нужно найти вероятность того, что два (или больше) независимых события произойдут подряд?
Допустим мы хотим знать, какова вероятность того, что бросая монетку раза, мы два раза увидим орла?
Мы уже считали – .
А если бросаем монетку раза? Какова вероятность увидеть орла раза подряд?
Всего возможных вариантов:
- Орел-орел-орел
- Орел-орел-решка
- Орел-решка-орел
- Орел-решка-решка
- Решка-орел-орел
- Решка-орел-решка
- Решка-решка-орел
- Решка-решка-решка
Не знаю как ты, но я раза ошибся, составляя этот список. Ух! А подходит нам только вариант (первый).
Для 5 бросков можешь составить список возможных исходов сам. Но математики не столь трудолюбивы, как ты.
Поэтому они сначала заметили, а потом доказали, что вероятность определенной последовательности независимых событий каждый раз уменьшается на вероятность одного события.
Другими словами,
Рассмотрим на примере все той же, злосчастной, монетки.
Вероятность выпадения орла в испытании? . Теперь мы бросаем монетку раз.
Какова вероятность выпадения раз подряд орла?
Это правило работает не только, если нас просят найти вероятность того, что произойдет одно и то же событие несколько раз подряд.
Если бы мы хотели найти последовательность РЕШКА-ОРЕЛ-РЕШКА, при бросках подряд, мы поступили бы также.
Вероятность выпадения решка – , орла – .
Вероятность выпадения последовательности РЕШКА-ОРЕЛ-РЕШКА-РЕШКА:
Можешь проверить сам, составив таблицу.
Правило сложения вероятностей несовместных событий.
Так стоп! Новое определение.
Давай разбираться. Возьмем нашу изношенную монетку и бросим её раза.
Возможные варианты:
- Орел-орел-орел
- Орел-орел-решка
- Орел-решка-орел
- Орел-решка-решка
- Решка-орел-орел
- Решка-орел-решка
- Решка-решка-орел
- Решка-решка-решка
Так вот несовместные события, это определенная, заданная последовательность событий. – это несовместные события.
Если мы хотим определить, какова вероятность двух (или больше) несовместных событий то мы складываем вероятности этих событий.
Нужно понять, что выпадение орла или решки – это два независимых события.
Если мы хотим определить, какова вероятность выпадения последовательности) (или любой другой), то мы пользуемся правилом умножения вероятностей.
Какова вероятность выпадения при первом броске орла, а при втором и третьем решки?
Но если мы хотим узнать, какова вероятность выпадения одной из нескольких последовательностей, например, когда орел выпадет ровно раз, т.е. варианты и, то мы должны сложить вероятности этих последовательностей.
Всего вариантов, нам подходит.
То же самое мы можем получить, сложив вероятности появления каждой последовательности:
Таким образом, мы складываем вероятности, когда хотим определить вероятность некоторых, несовместных, последовательностей событий.
Есть отличное правило, помогающее не запутаться, когда умножать, а когда складывать:
Возвратимся к примеру, когда мы подбросили монетку раза, и хотим узнать вероятность увидеть орла раз.
Что должно произойти?
Должны выпасть:
(орел И решка И решка) ИЛИ (решка И орел И решка) ИЛИ (решка И решка И орел).
Вот и получается:
Давай рассмотрим несколько примеров.
Пример 5.
В коробке лежит карандашей. красных, зеленых, оранжевых и желтых и черных. Какова вероятность вытащить красный или зеленый карандаши?
Решение:
Что должно произойти? Мы должны вытащить (красный ИЛИ зеленый).
Теперь понятно, складываем вероятности этих событий:
Ответ:
Пример 6.
Игральную кость бросают дважды, какова вероятность того, что в сумме выпадет 8 очков?
Решение.
Как мы можем получить очков?
(и) или (и) или (и) или (и) или (и).
Вероятность выпадения одной (любой) грани – .
Считаем вероятность:
Ответ:
Тренировка.
Думаю, теперь тебе стало понятно, когда нужно как считать вероятности, когда их складывать, а когда умножать. Не так ли? Давай немного потренируемся.
Задачи:
Возьмем карточную колоду, в которой карты, из них пик, червей, 13 треф и 13 бубен. От до туза каждой масти.
- Какова вероятность вытащить трефы подряд (первую вытащенную карту мы кладем обратно в колоду и перемешиваем)?
- Какова вероятность вытащить черную карту (пики или трефы)?
- Какова вероятность вытащить картинку (вальта, даму, короля или туза)?
- Какова вероятность вытащить две картинки подряд (первую вытащенную карту мы убираем из колоды)?
- Какова вероятность, взяв две карты, собрать комбинацию – (валет, дама или король) и туз Последовательность, в которой будут вытащены карты, не имеет значения.
Ответы:
- В колоде карты каждого достоинства, значит:
- События зависимы, так как после первой вытащенной карты количество карт в колоде уменьшилось (как и количество «картинок»). Всего вальтов, дам, королей и тузов в колоде изначально, а значит вероятность первой картой вытащить «картинку»:
Поскольку мы убираем из колоды первую карту, то значит в колоде осталось уже карта, из них картинок. Вероятность второй картой вытащить картинку:
Поскольку нас интересует ситуация, когда мы достаем из колоды: «картинку» И «картинку», то нужно перемножать вероятности:
Ответ:
- После первой вытащенной карты, количество карт в колоде уменьшится.Таким образом, нам подходит два варианта:
1) Первой картой вытаскиваем Туза, второй – валета, даму или короля
2) Первой картой вытаскиваем валета, даму или короля, второй – туза.Т.е. (туз и (валет или дама или король)) или ((валет или дама или король) и туз). Не забываем про уменьшение количества карт в колоде!
Если ты смог сам решить все задачи, то ты большой молодец! Теперь задачи на теорию вероятностей в ЕГЭ ты будешь щелкать как орешки!
ТЕОРИЯ ВЕРОЯТНОСТЕЙ. СРЕДНИЙ УРОВЕНЬ
Рассмотрим пример. Допустим, мы бросаем игральную кость. Что это за кость такая, знаешь? Так называют кубик с цифрами на гранях. Сколько граней, столько и цифр: от до скольки? До.
Итак, мы бросаем кость и хотим, чтобы выпало или. И нам выпадает.
В теории вероятностей говорят, что произошло благоприятное событие
(не путай с благополучным).
Если бы выпало, событие тоже было бы благоприятным. Итого может произойти всего два благоприятных события.
А сколько неблагоприятных? Раз всего возможных событий, значит, неблагоприятных из них события (это если выпадет или).
Определение:
Вероятностью называется отношение количества благоприятных событий к количеству всех возможных событий
. То есть вероятность показывает, какая доля из всех возможных событий приходится на благоприятные.
Обозначают вероятность латинской буквой (видимо, от английского слова probability – вероятность).
Принято измерять вероятность в процентах (см. тему , )
. Для этого значение вероятности нужно умножать на. В примере с игральной костью вероятность.
А в процентах: .
Примеры (реши сам):
- С какой вероятностью при бросании монетки выпадет орел? А с какой вероятностью выпадет решка?
- С какой вероятностью при бросании игральной кости выпадет четное число? А с какой – нечетное?
- В ящике простых, синих и красных карандашей. Наугад тянем один карандаш. Какова вероятность вытащить простой?
Решения:
- Сколько всего вариантов? Орел и решка – всего два. А сколько из них благоприятных? Только один – орел. Значит, вероятность
С решкой то же самое: .
- Всего вариантов: (сколько сторон у кубика, столько и различных вариантов). Благоприятных из них: (это все четные числа:).
Вероятность. С нечетными, естественно, то же самое. - Всего: . Благоприятных: . Вероятность: .
Полная вероятность
Все карандаши в ящике зеленые. Какова вероятность вытащить красный карандаш? Шансов нет: вероятность (ведь благоприятных событий -).
Такое событие называется невозможным
.
А какова вероятность вытащить зеленый карандаш? Благоприятных событий ровно столько же, сколько событий всего (все события – благоприятные). Значит, вероятность равна или.
Такое событие называется достоверным
.
Если в ящике зеленых и красных карандашей, какова вероятность вытащить зеленый или красный? Опять же. Заметим такую вещь: вероятность вытащить зеленый равна, а красный – .
В сумме эти вероятности равны ровно. То есть, сумма вероятностей всех возможных событий равна или.
Пример:
В коробке карандашей, среди них синих, красных, зеленых, простых, желтый, а остальные – оранжевые. Какова вероятность не
вытащить зеленый?
Решение:
Помним, что все вероятности в сумме дают. А вероятность вытащить зеленый равна. Значит, вероятность не вытащить зеленый равна.
Запомни этот прием:
вероятность того, что событие не произойдет равна минус вероятность того, что событие произойдет.
Независимые события и правило умножения
Ты кидаешь монетку раза, и хочешь, чтобы оба раза выпал орел. Какова вероятность этого?
Давай переберем все возможные варианты и определим, сколько их:
Орел-Орел, Решка-Орел, Орел-Решка, Решка-Решка. Какие еще?
Всего варианта. Из них нам подходит только один: Орел-Орел. Итого, вероятность равна.
Хорошо. А теперь кидаем монетку раза. Посчитай сам. Получилось? (ответ).
Ты мог заметить, что с добавлением каждого следующего броска вероятность уменьшается в раза. Общее правило называется правилом умножения
:
Вероятности независимых событий переменожаются.
Что такое независимые события? Все логично: это те, которые не зависят друг от друга. Например, когда мы бросаем монетку несколько раз, каждый раз производится новый бросок, результат которого не зависит от всех предыдущих бросков. С таким же успехом мы можем бросать одновременно две разные монетки.
Еще примеры:
- Игральную кость бросают дважды. Какова вероятность, что оба раза выпадет?
- Монетку бросают раза. Какова вероятность, что в первый раз выпадет орел, а потом два раза решка?
- Игрок бросает две кости. Какова вероятность, что сумма чисел на них будет равна?
Ответы:
- События независимы, значит, работает правило умножения: .
- Вероятность орла равна. Вероятность решки – тоже. Перемножаем:
- 12 может получиться только, если выпадут две -ки: .
Несовместные события и правило сложения
Несовместными
называются события, которые дополняют друг друга до полной вероятности. Из названия видно, что они не могут произойти одновременно. Например, если бросаем монетку, может выпасть либо орел, либо решка.
Пример.
В коробке карандашей, среди них синих, красных, зеленых, простых, желтый, а остальные – оранжевые. Какова вероятность вытащить зеленый или красный?
Решение
.
Вероятность вытащить зеленый карандаш равна. Красный – .
Благоприятных событий всего: зеленых + красных. Значит, вероятность вытащить зеленый или красный равна.
Эту же вероятность можно представить в таком виде: .
Это и есть правило сложения:
вероятности несовместных событий складываются.
Задачи смешанного типа
Пример.
Монетку бросают два раза. Какова вероятность того, что результат бросков будет разный?
Решение
.
Имеется в виду, что если первым выпал орел, второй должна быть решка, и наоборот. Получается, что здесь две пары независимых событий, и эти пары друг с другом несовместны. Как бы не запутаться, где умножать, а где складывать.
Есть простое правило для таких ситуаций. Попробуй описать, что должно произойти, соединяя события союзами «И» или «ИЛИ». Например, в данном случае:
Должны выпасть (орел и решка) или (решка и орел).
Там где стоит союз «и», будет умножение, а там где «или» – сложение:
Попробуй сам:
- С какой вероятностью при двух бросаниях монетки оба раза выпадет одно и та же сторона?
- Игральную кость бросают дважды. Какова вероятность, что в сумме выпадет очков?
Решения:
- (Выпал орел и
выпал орел) или
(выпала решка и
выпала решка): . - Какие есть варианты? и. Тогда:
Выпало (и) или (и) или (и): .
Еще пример:
Бросаем монетку раза. Какова вероятность, что хотя-бы один раз выпадет орел?
Решение:
Ой, как же не хочется перебирать варианты… Орел-решка-решка, Орел-орел-решка, … А и не надо! Вспоминаем про полную вероятность. Вспомнил? Какова вероятность, что орел не выпадет ни разу
? Это же просто: все время летят решки, значит.
ТЕОРИЯ ВЕРОЯТНОСТЕЙ. КОРОТКО О ГЛАВНОМ
Вероятность
– это отношение количества благоприятных событий к количеству всех возможных событий.
Независимые
события
Два события независимы если при наступлении одного вероятность наступления другого не изменяется.
Полная вероятность
Вероятность всех возможных событий равна ().
Вероятность того, что событие не произойдет, равна минус вероятность того, что событие произойдет.
Правило умножения вероятностей независимых событий
Вероятность определенной последовательности независимых событий, равна произведению вероятностей каждого из событий
Несовместные
события
Несовместными называются события, которые никак не могут произойти одновременно в результате эксперимента. Ряд несовместных событий образуют полную группу событий.
Вероятности несовместных событий складываются.
Описав что должно произойти, используя союзы «И» или «ИЛИ», вместо «И» ставим знак умножения, а вместо «ИЛИ» — сложения.
Ну вот, тема закончена. Если ты читаешь эти строки, значит ты очень крут.
Потому что только 5% людей способны освоить что-то самостоятельно. И если ты дочитал до конца, значит ты попал в эти 5%!
Теперь самое главное.
Ты разобрался с теорией по этой теме. И, повторюсь, это… это просто супер! Ты уже лучше, чем абсолютное большинство твоих сверстников.
Проблема в том, что этого может не хватить…
Для чего?
Для успешной сдачи ЕГЭ, для поступления в институт на бюджет и, САМОЕ ГЛАВНОЕ, для жизни.
Я не буду тебя ни в чем убеждать, просто скажу одну вещь…
Люди, получившие хорошее образование, зарабатывают намного больше, чем те, кто его не получил. Это статистика.
Но и это – не главное.
Главное то, что они БОЛЕЕ СЧАСТЛИВЫ (есть такие исследования). Возможно потому, что перед ними открывается гораздо больше возможностей и жизнь становится ярче? Не знаю…
Но, думай сам…
Что нужно, чтобы быть наверняка лучше других на ЕГЭ и быть в конечном итоге… более счастливым?
НАБИТЬ РУКУ, РЕШАЯ ЗАДАЧИ ПО ЭТОЙ ТЕМЕ.
На экзамене у тебя не будут спрашивать теорию.
Тебе нужно будет решать задачи на время
.
И, если ты не решал их (МНОГО!), ты обязательно где-нибудь глупо ошибешься или просто не успеешь.
Это как в спорте – нужно много раз повторить, чтобы выиграть наверняка.
Найди где хочешь сборник, обязательно с решениями, подробным разбором
и решай, решай, решай!
Можно воспользоваться нашими задачами (не обязательно) и мы их, конечно, рекомендуем.
Для того, чтобы набить руку с помощью наших задач нужно помочь продлить жизнь учебнику YouClever, который ты сейчас читаешь.
Как? Есть два варианта:
- Открой доступ ко всем скрытым задачам в этой статье – 299 руб.
- Открой доступ ко всем скрытым задачам во всех 99-ти статьях учебника – 999 руб.
Да, у нас в учебнике 99 таких статей и доступ для всех задач и всех скрытых текстов в них можно открыть сразу.
Во втором случае мы подарим тебе
тренажер “6000 задач с решениями и ответами, по каждой теме, по всем уровням сложности”. Его точно хватит, чтобы набить руку на решении задач по любой теме.
На самом деле это намного больше, чем просто тренажер – целая программа подготовки. Если понадобится, ты сможешь ею так же воспользоваться БЕСПЛАТНО.
Доступ ко всем текстам и программам предоставляется на ВСЕ время существования сайта.
И в заключение…
Если наши задачи тебе не нравятся, найди другие. Только не останавливайся на теории.
“Понял” и “Умею решать” – это совершенно разные навыки. Тебе нужны оба.
Найди задачи и решай!
Знать, как оценить вероятность того или иного события на основе коэффициентов, крайне важно для выбора правильной ставки. Если вы не понимаете, как перевести букмекерский коэффициент в вероятность, то никогда не сможете определить, как соотносится букмекерский коэффициент с реальными шансами того, что событие состоится. Следует понимать, если вероятность события по версии букмекеров ниже, чем вероятность этого же события по вашей собственной версии, ставка на это событие будет ценной. Сравнить коэффициенты на разные события можно на сайте Odds.ru .
1.1. Типы коэффициентов
Букмекерские конторы, как правило, предлагают три типа коэффициентов – десятичный, дробный и американский. Разберем каждую из разновидностей.
1.2. Десятичные коэффициенты
Десятичные коэффициенты при умножении на размер ставки позволяют рассчитать всю сумму, которую вы получите на руки в случае выигрыша. К примеру, если вы поставили 1 доллар на коэффициент 1,80, в случае выигрыша вы получите 1 доллар 80 центов (1 доллар – возвращенная сумма ставки, 0,80 – выигрыш по ставке, он же ваша чистая прибыль).
То есть вероятность исхода, по версии букмекеров, составляет 55%.
1.3. Дробные коэффициенты
Дробные коэффициенты – наиболее традиционный вид коэффициентов. В числителе показана потенциальная сумма чистого выигрыша. В знаменателе – сумма ставки, которую нужно сделать, чтобы этот самый выигрыш получить. К примеру, коэффициент 7/2 означает, что для того, чтобы получить чистый выигрыш в размере 7 долларов, вам необходимо поставить 2 доллара.
Для того чтобы рассчитать вероятность события на основе десятичного коэффициента, следует провести простые вычисления – знаменатель разделить на сумму числителя и знаменателя. Для вышеобозначенного коэффициента 7/2 расчет будет таким:
2 / (7+2) = 2 / 9 = 0,22
То есть вероятность исхода, по версии букмекеров, составляет 22%.
1.4. Американские коэффициенты
Данный вид коэффициентов популярен в Северной Америке. На первый взгляд, они кажутся довольно сложными и непонятными, но не стоит пугаться. Понимание американских коэффициентов может вам пригодиться, например, при игре в американских казино, для понимания котировок, демонстрируемых в североамериканских спортивных трансляциях. Разберем, как оценить вероятность исхода на основе американских коэффициентов.
В первую очередь надо понимать, что американские коэффициенты бывают положительными и отрицательными. Отрицательный американский коэффициент всегда идет в формате, к примеру, «-150». Это означает, что для того, чтобы получить 100 долларов чистой прибыли (выигрыш), необходимо поставить 150 долларов.
Положительный американский коэффициент рассчитывается наоборот. К примеру, у нас есть коэффициент «+120». Это означает, что для того, чтобы получить 120 долларов чистой прибыли (выигрыш), вам необходимо поставить 100 долларов.
Расчет вероятности на основе отрицательных американских коэффициентов делается по следующей формуле:
(-(отрицательный американский коэффициент)) / ((-(отрицательный американский коэффициент)) + 100)
(-(-150)) / ((-(-150)) + 100) = 150 / (150 + 100) = 150 / 250 = 0,6
То есть вероятность события, на которое дается отрицательный американский коэффициент «-150», составляет 60%.
Теперь рассмотрим аналогичные вычисления для положительного американского коэффициента. Вероятность в этом случае рассчитывается по следующей формуле:
100 / (положительный американский коэффициент + 100)
100 / (120 + 100) = 100 / 220 = 0.45
То есть вероятность события, на которое дается положительный американский коэффициент «+120», составляет 45%.
1.5. Как переводить коэффициенты из одного формата в другой?
Умение переводить коэффициенты из одного формата в другой может впоследствии сослужить вам хорошую службу. Как ни странно, до сих пор есть конторы, в которых коэффициенты не конвертируются и показаны лишь в одном, непривычном для нас формате. Рассмотрим на примерах, как это делать. Но для начала нам надо научиться вычислять вероятность исхода на основе данного нам коэффициента.
1.6. Как на основе вероятности рассчитать десятичный коэффициент?
Здесь все очень просто. Необходимо 100 разделить на вероятность события в процентном отношении. То есть, если предполагаемая вероятность события составляет 60%, вам надо:
При предполагаемой вероятности события в 60% десятичный коэффициент будет составлять 1,66.
1.7. Как на основе вероятности рассчитать дробный коэффициент?
В данном случае необходимо 100 разделить на вероятность события и от полученного результата отнять единицу. К примеру, вероятность события составляет 40%:
(100 / 40) — 1 = 2,5 — 1 = 1,5
То есть мы получаем дробный коэффициент 1,5/1 или, для удобства счета, – 3/2.
1.8. Как на основе вероятного исхода рассчитать американский коэффициент?
Здесь многое будет зависеть от вероятности события – будет ли она более 50% или менее. Если вероятность события более 50%, то расчет будет производиться по такой формуле:
— ((вероятность) / (100 — вероятность)) * 100
Например, если вероятность события составляет 80%, то:
— (80 / (100 — 80)) * 100 = — (80 / 20) * 100 = -4 * 100 = (-400)
При предполагаемой вероятности события в 80% мы получили отрицательный американский коэффициент «-400».
Если вероятность события менее 50 процентов, то формула будет следующей:
((100 — вероятность) / вероятность) * 100
Например, если вероятность события составляет 40%, то:
((100-40) / 40) * 100 = (60 / 40) * 100 = 1,5 * 100 = 150
При предполагаемой вероятности события в 40% мы получили положительный американский коэффициент «+150».
Эти вычисления помогут вам лучше понять концепцию ставок и коэффициентов, научиться оценивать истинную стоимость той или иной ставки.
1.3.1. Последовательность независимых испытаний (схема Бернулли)
Предположим,
что некоторый эксперимент можно проводить
неоднократно при одних и тех же условиях.
Пусть этот опыт производится n
раз, т. е. проводится последовательность
из n
испытаний.
Определение.
Последовательность
n
испытаний
называют взаимно
независимой
,
если любое событие, связанное с данным
испытанием, не зависит от любых событий,
относящихся к остальным испытаниям.
Допустим,
что некоторое событие A
может произойти с вероятностью p
в результате одного испытанияили
не произойти с вероятностью q
=
1–
p
.
Определение
.
Последовательность из n
испытаний
образует схему Бернулли, если выполняются
следующие условия:
последовательность
n
испытаний взаимно независима,
2)
вероятность события A
не изменяется от испытания к испытанию
и не зависит от результата в других
испытаниях.
Событие
A
называют “ успехом” испытания, а
противоположное событие
– “неудачей”. Рассмотрим событие
={
в
n
испытаниях произошло ровно
m
“успехов”}.
Для вычисления
вероятности этого события справедлива
формула Бернулли
p
(
)
=
,
m
= 1, 2, …,
n
, (1.6)где
– число сочетаний из
n
элементов по
m
:
=
=
.
Пример
1.16.
Три раза подбрасывают кубик. Найти:
а) вероятность
того, что 6 очков выпадет два раза;
б) вероятность
того, что число шестерок не появится
более двух раз.
Решение
.
“Успехом”
испытания будем считать выпадение на
кубике грани с изображением 6 очков.
а)
Общее число испытаний – n
=3,
число “успехов” – m
=
2. Вероятность “успеха” – p
=,
а вероятность “неудачи” – q=
1 –
=.
Тогда по формуле Бернулли вероятность
того, что результате трехразового
бросания кубика два раза выпадет сторона
с шестью очками, будет равна
.б)
Обозначим через
А
событие, которое заключается в том, что
грань с числом очков 6 появится не более
двух раз. Тогда событие можно представить
в виде
суммы
трех несовместных
событий
А=
,
где
В
3 0
– событие, когда интересующая грань
ни разу не появится,
В
3 1
– событие, когда интересующая грань
появится один раз,
В
3 2
– событие, когда интересующая грань
появится два раза.
По формуле Бернулли
(1.6) найдем
p
(
А
)
=
р (
)
=
p
(
)
=
+
+
=
=
.
1.3.2. Условная вероятность события
Условная
вероятность отражает влияние одного
события на вероятность другого. Изменение
условий, в которых проводится эксперимент,
также влияет
на вероятность
появления интересующего события.
Определение.
Пусть
A
и
B
– некоторые события, и вероятность
p
(B
)>
0.
Условной
вероятностью
события A
при условии, что “событие B
ужепроизошло”
называется отношение вероятности
произведения данных событий к вероятности
события, которое произошло раньше, чем
событие, вероятность которого требуется
найти. Условная вероятность обозначается
как p
(A
B
).
Тогда
по определению
p
(
A
B
)
=
.
(1.7)
Пример
1.17.
Подбрасывают
два кубика. Пространство элементарных
событий состоит из упорядоченных пар
чисел
(1,1)
(1,2) (1,3) (1,4) (1,5) (1,6)
(2,1)
(2,2) (2,3) (2,4) (2,5) (2,6)
(3,1)
(3,2) (3,3) (3,4) (3,5) (3,6)
(4,1)
(4,2) (4,3) (4,4) (4,5) (4,6)
(5,1)
(5,2) (5,3) (5,4) (5,5) (5,6)
(6,1)
(6,2) (6,3) (6,4) (6,5) (6,6).
В
примере 1.16 было установлено, что событие
A
={число очков на первом кубике > 4} и
событие C
={сумма очков равна 8} зависимы. Составим
отношение
.
Это
отношение можно интерпретировать
следующим образом. Допустим, что о
результате первого бросания известно,
что число очков на первом кубике > 4.
Отсюда следует, что бросание второго
кубика может привести к одному из 12
исходов, составляющих событие A
:
(5,1) (5,2) (5,3) (5,4)
(5,5) (5,6)
(6,1) (6,2) (6,3) (6,4)
(6,5) (6,6) .
При
этом событию
C
могут соответствовать только два из
них (5,3) (6,2). В этом случае вероятность
события
C
будет
равна
.
Таким образом, информация о наступлении
события
A
оказала влияние на вероятность события
C
.
Вероятность
произведения событий
Теорема
умножения
Вероятность
произведения событий
A
1
A
2
A
n
определяется формулой
p
(A
1
A
2
A
n
)
= p
(A
1)
p
(A
2
A
1))
p
(A
n
A
1 A
2
A
n-
1).(1.8)
Для произведения
двух событий отсюда следует, что
p
(AB
)
= p
(A
B)
p
{B
)
= p
(B
A
)
p
{A
).
(1.9)
Пример
1.18.
В
партии из 25 изделий 5 изделий бракованных.
Последовательно наугад выбирают 3
изделия. Определить вероятность того,
что все выбранные изделия бракованные.
Решение.
Обозначим события:
A
1
=
{первое изделие бракованное},
A
2
=
{второе изделие бракованное},
A
3
=
{третье изделие бракованное},
A
=
{все изделия бракованные}.
Событие
А
есть
произведение трех событий A
=
A
1
A
2
A
3
.
Из
теоремы умножения (1.6) получим
p
(A
)= р(A
1
A
2
A
3
) =
p
(A
1)p
(A
2
A
1))p
(A
3
A
1 A
2).
Классическое
определение вероятности позволяет
найти p
(A
1)
– это отношение числа бракованных
изделий к общему количеству изделий:
p
(A
1)=
;
p
(A
2)
–
этоотношение
числа бракованных изделий, оставшихся
после изъятия одного, к общему числу
оставшихся изделий:
p
(A
2
A
1))=
;
p
(A
3)
– это отношение
числа бракованных изделий, оставшихся
после изъятия двух бракованных, к общему
числу оставшихся изделий:
p
(A
3
A
1 A
2)=.
Тогда
вероятность события A
будет
равна
p
(A
)
==
.
Профессиональный беттер должен хорошо ориентироваться в коэффициентах, быстро и правильно оценивать вероятность события по коэффициенту
и при необходимости уметь перевести коэффициенты из одного формата в другой
. В данном мануале мы расскажем о том, какие бывают виды коэффициентов, а так же на примерах разберём, как можно высчитывать вероятность по известному коэффициенту
и наоборот.
Какие бывают типы коэффициентов?
Существует три основных вида коэффициентов, которые предлагают игрокам букмекеры: десятичные коэффициенты
, дробные коэффициенты
(английские) и американские коэффициенты
. Наиболее распространённые коэффициенты в Европе – десятичные. В Северной Америке популярны американские коэффициенты. Дробные коэффициенты – наиболее традиционный вид, они сразу же отражают информацию о том сколько нужно поставить, чтобы получить определённую сумму.
Десятичные коэффициенты
Десятичные
или еще их называют европейские коэффициенты
– это привычный формат числа, представленный десятичной дробью с точностью до сотых, а иногда даже до тысячных. Пример десятичного коэффициента – 1.91. Рассчитать прибыль в случае с десятичными коэффициентами очень просто, достаточно лишь умножить сумму вашей ставки на этот коэффициент. Например, в матче “Манчестер Юнайтед” – “Арсенал” победа “МЮ” выставлена с коэффициентом – 2.05, ничья оценена коэффициентом – 3.9, а победа “Арсенала” равняется – 2.95. Предположим, что мы уверены в победе “Юнайтед” и ставим на них 1000 долларов. Тогда наш возможный доход рассчитывается следующим образом:
2.05 * $1000 = $2050;
Правда ведь ничего сложного?! Точно так же рассчитывается возможный доход при ставке на ничью и победу “Арсенала”.
Ничья: 3.9 * $1000 = $3900;
Победа “Арсенала”: 2.95 * $1000 = $2950;
Как рассчитать вероятность события по десятичным коэффициентам?
Представим теперь что нам нужно определить вероятность события по десятичным коэффициентам, которые выставил букмекер. Делается это так же очень просто. Для этого мы единицу делим на этот коэффициент.
Возьмем уже имеющиеся данные и посчитаем вероятность каждого события:
Победа “Манчестер Юнайтед”: 1 / 2.05 = 0,487 = 48,7%;
Ничья: 1 / 3.9 = 0,256 = 25,6%;
Победа “Арсенала”: 1 / 2.95 = 0,338 = 33,8%;
Дробные коэффициенты (Английские)
Как понятно из названия дробный коэффициент
представлен обыкновенной дробью. Пример английского коэффициента – 5/2. В числителе дроби находиться число, являющееся потенциальной суммой чистого выигрыша, а в знаменателе расположено число обозначающее сумму которую нужно поставить, чтобы этот выигрыш получить. Проще говоря, мы должны поставить $2 доллара, чтобы выиграть $5. Коэффициент 3/2 означает что для того чтобы получить $3 чистого выигрыша нам придётся сделать ставку в размере $2.
Как рассчитать вероятность события по дробным коэффициентам?
Вероятность события по дробным коэффициентам рассчитать так же не сложно, нужно всего на всего разделить знаменатель на сумму числителя и знаменателя.
Для дроби 5/2 рассчитаем вероятность: 2 / (5+2) = 2 / 7 = 0,28 = 28%;
Для дроби 3/2 рассчитаем вероятность:
Американские коэффициенты
Американские коэффициенты
в Европе непопулярны, зато в Северной Америке очень даже. Пожалуй, данный вид коэффициентов самый сложный, но это только на первый взгляд. На самом деле и в этом типе коэффициентов ничего сложного нет. Сейчас во всем разберёмся по порядку.
Главной особенностью американских коэффициентов является то, что они могут быть как положительными
, так и отрицательными
. Пример американских коэффициентов – (+150), (-120). Американский коэффициент (+150) означает, что для того чтобы заработать $150 нам нужно поставить $100. Иными словами положительный американский коэффициент отражает потенциальный чистый заработок при ставке в $100. Отрицательный же американский коэффициент отражает сумму ставки, которую необходимо сделать для того чтобы получить чистый выигрыш в $100. Например коэффициент (- 120) нам говорит о том, что поставив $120 мы выиграем $100.
Как рассчитать вероятность события по американским коэффициентам?
Вероятность события по американскому коэффициенту считается по следующим формулам:
(-(M)) / ((-(M)) + 100)
, где M – отрицательный американский коэффициент;
100 / (P + 100)
, где P – положительный американский коэффициент;
Например, мы имеем коэффициент (-120), тогда вероятность рассчитывается так:
(-(M)) / ((-(M)) + 100); подставляем вместо “M” значение (-120);
(-(-120)) / ((-(-120)) + 100 = 120 / (120 + 100) = 120 / 220 = 0,545 = 54,5%;
Таким образом, вероятность события с американским коэффициентом (-120) равна 54,5%.
Например, мы имеем коэффициент (+150), тогда вероятность рассчитывается так:
100 / (P + 100); подставляем вместо “P” значение (+150);
100 / (150 + 100) = 100 / 250 = 0,4 = 40%;
Таким образом, вероятность события с американским коэффициентом (+150) равна 40%.
Как зная процент вероятности перевести его в десятичный коэффициент?
Для того чтобы рассчитать десятичный коэффициент по известному проценту вероятности нужно 100 разделить на вероятность события в процентах. Например, вероятность события составляет 55%, тогда десятичный коэффициент этой вероятности будет равен 1,81.
100 / 55% = 1,81
Как зная процент вероятности перевести его в дробный коэффициент?
Для того чтобы рассчитать дробный коэффициент по известному проценту вероятности нужно от деления 100 на вероятность события в процентах отнять единицу. Например, имеем процент вероятности 40%, тогда дробный коэффициент этой вероятности будет равен 3/2.
(100 / 40%) – 1 = 2,5 – 1 = 1,5;
Дробный коэффициент равен 1,5/1 или 3/2.
Как зная процент вероятности перевести его в американский коэффициент?
Если вероятность события больше 50%, то расчёт производится по формуле:
– ((V) / (100 – V)) * 100, где V – вероятность;
Например, имеем вероятность события 80%, тогда американский коэффициент этой вероятности будет равен (-400).
– (80 / (100 – 80)) * 100 = – (80 / 20) * 100 = – 4 * 100 = (-400);
В случае если вероятность события меньше 50%, то расчёт производиться по формуле:
((100 – V) / V) * 100
, где V – вероятность;
Например, имеем процент вероятности события 20%, тогда американский коэффициент этой вероятности будет равен (+400).
((100 – 20) / 20) * 100 = (80 / 20) * 100 = 4 * 100 = 400;
Как перевести коэффициент в другой формат?
Бывают случаи, когда необходимо перевести коэффициенты из одного формата в другой. Например, у нас есть дробный коэффициент 3/2 и нам нужно перевести его в десятичный. Для перевода дробного коэффициента в десятичный мы сначала определяем вероятность события с дробным коэффициентом, а затем эту вероятность переводим в десятичный коэффициент.
Вероятность события с дробным коэффициентом 3/2 равна 40%.
2 / (3+2) = 2 / 5 = 0,4 = 40%;
Теперь переведём вероятность события в десятичный коэффициент, для этого 100 делим на вероятность события в процентах:
100 / 40% = 2.5;
Таким образом, дробный коэффициент 3/2 равен десятичному коэффициенту 2.5. Аналогичным образом переводятся, например, американские коэффициенты в дробные, десятичные в американские и т.д. Самое сложное во всём этом лишь расчёты.
