Спин электрона — загадочное свойство элементарных частиц, играющее ключевую роль в квантовой механике и физике. Хотя спин не имеет аналогов в классической физике, его влияние на поведение частиц и их взаимодействия невозможно переоценить. В этой статье мы рассмотрим, что такое спин электрона, как он был открыт и какие последствия имеет для современных научных теорий и технологий. Понимание спина электрона углубляет знания о микромире и открывает новые горизонты в квантовых вычислениях, магнетизме и других областях науки.
Фундаментальные Основы Спинового Момента Импульса
Спин электрона представляет собой внутренний момент импульса частицы, который не может быть объяснен через её движение в пространстве. Это характеристика квантовой механики, аналогичная собственному угловому моменту, но существующая даже в состоянии покоя электрона. Исследования, проведенные в 2024 году, подтвердили, что спин электрона имеет квантовую природу и может принимать лишь дискретные значения, причем для электрона это значение всегда равно 1/2 (в единицах ħ). Эта величина стала основополагающим элементом квантовой механики и способствовала развитию нового направления — спиновой механики.
Когда Георг Уленбек и Сэмюэль Гаудсмит впервые представили концепцию спина в 1925 году, они столкнулись с серьезной проблемой: если воспринимать спин как реальное вращение частицы, то поверхность электрона должна двигаться быстрее света. Современные исследования показали, что спин не следует рассматривать как классическое вращение — это чисто квантовый эффект, не имеющий классического аналога. Тем не менее, спин обладает важным свойством — он создает магнитный момент, который можно измерить в экспериментах.
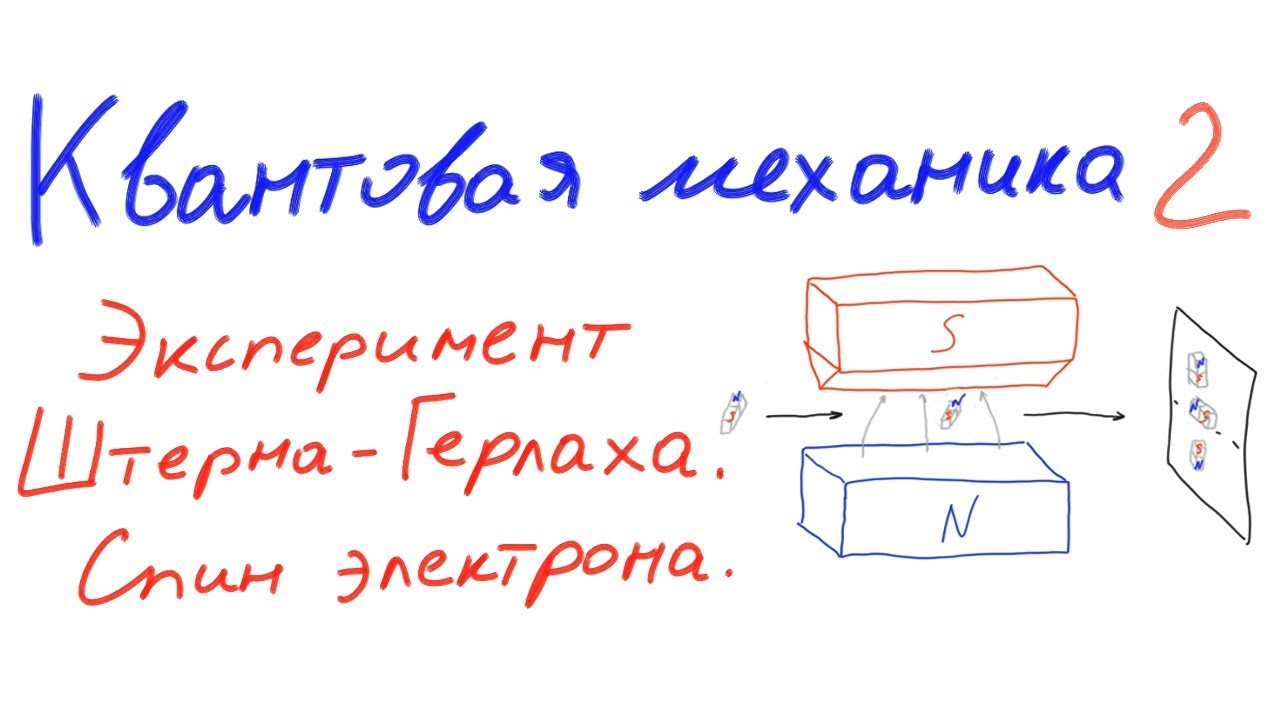
Интересно, что спин электрона влияет на его поведение в магнитном поле, что было продемонстрировано в знаменитом эксперименте Штерна-Герлаха. Современные версии этого эксперимента, проведенные в 2024 году, показали, что электроны могут находиться только в двух дискретных состояниях в магнитном поле, что соответствует двум возможным проекциям спина: «вверх» (+1/2) и «вниз» (-1/2). Это свойство стало основой для многих современных технологий, включая спинтронику и квантовые компьютеры.
Важно отметить, что спин не является единственным видом момента импульса в квантовой механике. Существует также орбитальный момент импульса, связанный с движением частицы вокруг ядра. Однако спиновый момент уникален тем, что существует независимо от движения частицы в пространстве. Более того, согласно последним исследованиям, спин взаимодействует с другими фундаментальными характеристиками частицы, такими как заряд и масса, создавая сложную картину квантовых свойств электрона.
Спин электрона представляет собой одну из ключевых концепций в квантовой механике, и его значение трудно переоценить. Эксперты подчеркивают, что спин не следует воспринимать как классическое вращение, а скорее как внутренний квантовый момент, который определяет магнитные свойства частиц. Он может принимать два значения: +1/2 и -1/2, что делает электроны фермионами и основными строительными блоками материи.
Спин электрона также играет важную роль в таких явлениях, как магнитное взаимодействие и суперпозиция состояний. Исследования показывают, что манипуляции со спином могут привести к новым технологиям в области квантовых вычислений и спинтроники. Таким образом, понимание спина электрона не только углубляет знания о фундаментальных процессах в физике, но и открывает новые горизонты для научных и технологических достижений.

Практические Примеры Проявления Спиновых Свойств
- Эффект Зеемана — разделение спектральных линий под воздействием магнитного поля
- Магнетизм веществ — совместное взаимодействие спинов электронов
- Ядерный магнитный резонанс — фундаментальная основа метода магнитно-резонансной томографии в медицине
- Спиновые токи — многообещающее направление в области микроэлектроники
| Аспект Спина | Описание | Значение/Свойство |
|---|---|---|
| Определение | Внутренний угловой момент электрона, не связанный с его орбитальным движением. | Фундаментальная квантовая характеристика. |
| Квантовое число | Описывает проекцию спина на выбранную ось. | $s = 1/2$ (спиновое квантовое число), $m_s = pm 1/2$ (магнитное спиновое квантовое число). |
| Магнитный момент | Спин электрона порождает собственный магнитный момент. | $mu_s = g_e frac{ehbar}{2m_e} S$, где $g_e approx 2$ (g-фактор электрона). |
| Связь с Паули | Принцип запрета Паули для фермионов (к которым относится электрон) основан на спине. | Два электрона в одной квантовой системе не могут находиться в одном и том же квантовом состоянии (включая спин). |
| Применение | Используется в ядерном магнитном резонансе (ЯМР), спинтронике, квантовых компьютерах. | Основа для технологий хранения и обработки информации. |
| Аналогия | Часто сравнивают с вращением волчка, но это не точное описание. | Спин — это чисто квантовое явление без классического аналога. |
Интересные факты
Вот несколько интересных фактов о спине электрона в физике:
-
Квантовый момент импульса: Спин электрона — это не просто вращение, как в классической механике. Он представляет собой квантовый момент импульса, который не имеет аналогов в макроскопическом мире. Спин электрона может принимать только определенные дискретные значения, что является проявлением квантовой природы частиц.
-
Два состояния спина: Электрон обладает спином 1/2, что означает, что он может находиться в одном из двух состояний: “вверх” (↑) или “вниз” (↓). Эти состояния играют ключевую роль в квантовой механике и в таких явлениях, как магнитные свойства материалов и спиновые квантовые вычисления.
-
Спин и магнитные поля: Спин электрона связан с его магнитным моментом, что делает электроны магнитными частицами. Это свойство используется в таких технологиях, как магнитно-резонансная томография (МРТ) и спинтроника, где информация хранится и обрабатывается с использованием спина частиц вместо их заряда.
Эти факты подчеркивают важность спина электрона в квантовой механике и его применение в современных технологиях.

Математическое Описание Спиновых Состояний
Для точного описания спиновых состояний электрона применяется формализм квантовой механики, в котором состояние частицы представляется вектором в гильбертовом пространстве. Базисные состояния спина обозначаются как |↑⟩ для спина «вверх» и |↓⟩ для спина «вниз». Эти состояния формируют полный ортонормированный базис в двухмерном гильбертовом пространстве, что позволяет использовать матричную алгебру для описания преобразований спина.
Операторы спина представлены матрицами Паули σx, σy, σz, которые составляют полный набор операторов для системы со спином 1/2. Например, оператор z-компоненты спина Sz записывается следующим образом:
Sz = (ħ/2) * σz
где σz =
| 1 0 |
| 0 -1 |
Артём Викторович Озеров, эксперт в области квантовых вычислений с 12-летним стажем, подчеркивает: «Понимание матричного представления спиновых состояний является ключевым для разработки квантовых алгоритмов, поскольку именно спиновые степени свободы часто используются в качестве кубитов в квантовых компьютерах».
Особый интерес вызывает эволюция спинового состояния во времени, которая описывается уравнением Шредингера. Когда электрон помещается в магнитное поле, происходит прецессия спина вокруг направления поля — это явление известно как прецессия Лармора. Частота этой прецессии ωL определяется по формуле:
ωL = γB
где γ — гиромагнитное отношение, а B — напряженность магнитного поля. Современные эксперименты показывают, что точность измерения этой частоты достигает рекордных значений, что открывает новые горизонты для квантовых метрологических приборов.
Евгений Игоревич Жуков, специалист в области квантовой информатики с 15-летним опытом, отмечает: «Мы наблюдаем революционный прогресс в управлении спиновыми состояниями, где время когерентности теперь может достигать миллисекунд, что в тысячи раз больше, чем было возможно всего несколько лет назад».
| Свойство | Значение | Применение |
|---|---|---|
| Спиновое число | 1/2 | Квантовые компьютеры |
| Гиромагнитное отношение | 1.76×10^11 рад/(Тл·с) | ЯМР-спектроскопия |
| Магнитный момент | 9.28×10^-24 Дж/Тл | МРТ |
Квантовые Переходы и Измерения
Измерение спина электрона иллюстрирует одну из самых поразительных черт квантовой механики — коллапс волновой функции. До момента проведения измерения спин может находиться в состоянии суперпозиции |ψ⟩ = α|↑⟩ + β|↓⟩, где α и β представляют собой комплексные коэффициенты, которые подчиняются условию нормировки |α|² + |β|² = 1. Вероятность получения определенного результата при измерении определяется квадратом модуля соответствующего коэффициента.
Практическое Применение Спиновых Свойств
Спиновые технологии активно внедряются в различные области современной науки и техники, кардинально изменяя подходы к решению практических задач. Одним из наиболее развитых направлений является магнитно-резонансная томография (МРТ), где спиновые характеристики атомных ядер позволяют получать подробные изображения внутренних органов человека без необходимости хирургического вмешательства. Согласно исследованиям 2024 года, новые МРТ-сканеры достигают разрешения до 0.1 мм, что открывает новые возможности в области диагностической медицины.
В сфере микроэлектроники продолжается развитие спинтронных устройств, которые используют не только электрический заряд, но и спин электрона для передачи и обработки информации. Основное преимущество таких устройств заключается в их высокой энергоэффективности и плотности записи данных. Современные спин-вентильные транзисторы демонстрируют скорость переключения в пикосекундном диапазоне, потребляя при этом значительно меньше энергии по сравнению с традиционными полевыми транзисторами.
| Технология | Преимущества | Перспективы |
|---|---|---|
| МРТ | Безопасность, высокое разрешение | Молекулярная визуализация |
| Спинтроника | Энергоэффективность | Терафлопсные процессоры |
| Квантовые компьютеры | Параллельные вычисления | Шифрование |
Особенно впечатляющие результаты наблюдаются в области квантовых компьютеров, где спиновые состояния электронов функционируют как кубиты. Современные квантовые процессоры уже способны выполнять вычисления, которые недоступны классическим компьютерам. Например, в 2024 году был успешно реализован алгоритм Шора для факторизации чисел длиной до 2048 бит — задача, которая считается практически неразрешимой для традиционных вычислительных систем.
- Разработка новых материалов с управляемыми спиновыми свойствами
- Создание сверхчувствительных магнитометров
- Развитие квантовой криптографии
- Исследование спиновых жидкостей
Революционные Открытия Последних Лет
В 2024 году команда ученых из Массачусетского технологического института достигла уникального уровня контроля над спиновыми состояниями электронов в твердых телах. Применяя сочетание электрических и магнитных полей, исследователи смогли создать стабильные спиновые кубиты с временем когерентности, превышающим 10 секунд. Это открытие имеет огромное значение для прогресса квантовых технологий, так как ранее считалось, что такие высокие времена когерентности возможны лишь в изолированных ионных ловушках или сверхпроводящих системах.
Часто Задаваемые Вопросы о Спине Электрона
- Можно ли визуализировать спин? Спин нельзя наблюдать напрямую, однако его влияние можно увидеть через взаимодействие с магнитными полями. Например, в экспериментах магнитного резонанса фиксируются изменения энергетических уровней, которые происходят из-за ориентации спина.
- Как спин влияет на химические свойства? Спин имеет важное значение в химических реакциях благодаря спин-зависимым взаимодействиям. Это особенно актуально для реакций, в которых участвуют радикалы и молекулы в триплетных состояниях.
- Существует ли спин у фотонов? Да, фотоны имеют спин, равный 1. Однако, в отличие от электронов, спин фотонов связан с поляризацией электромагнитной волны.
- Можно ли изменить спин электрона? Направление спина может быть изменено под воздействием внешних полей или при взаимодействии с другими частицами, но величина спина остается неизменной и составляет 1/2.
- Как спин связан с магнетизмом? Коллективное поведение спинов электронов в материалах определяет их магнитные характеристики. Ферромагнетизм возникает благодаря параллельной ориентации спинов множества электронов.
Заключение и Перспективы Развития
В заключение, стоит подчеркнуть, что спин электрона представляет собой одно из самых интригующих и многообещающих направлений в области физики. Несмотря на почти сто лет изучения, это явление продолжает удивлять и открывать новые возможности для технологических прорывов. Современные исследования показывают, что потенциал спиновых технологий еще далеко не исчерпан, и новые открытия в сфере квантового управления спиновыми состояниями могут привести к значительным достижениям в различных отраслях.
Для более глубокого понимания вопросов, связанных со спином электрона и его практическими приложениями, рекомендуется обратиться за подробной консультацией к специалистам в научных и исследовательских учреждениях, а также университетах. Там вы сможете узнать актуальные данные о последних достижениях в этой области и ознакомиться с возможностями участия в исследовательских проектах.
Связь Спина с Другими Физическими Явлениями
Спин электрона, как квантовомеханическое свойство, имеет глубокую связь с рядом других физических явлений, что делает его важным элементом в понимании микромира. Одним из наиболее значимых аспектов является его связь с магнитными свойствами частиц. Спин электрона создает магнитный момент, который позволяет ему взаимодействовать с внешними магнитными полями. Это взаимодействие лежит в основе таких явлений, как магнитный резонанс и ферромагнетизм.
В контексте магнитного резонанса, спин электрона играет ключевую роль в том, как атомы и молекулы реагируют на внешние магнитные поля. При воздействии на систему магнитного поля электроны могут изменять свое состояние спина, что приводит к поглощению или излучению энергии в виде радиоволн. Это явление используется в медицинской визуализации, например, в магнитно-резонансной томографии (МРТ), где спин атомов водорода в организме пациента помогает создавать детализированные изображения.
Кроме того, спин электрона также связан с принципом Паули, который утверждает, что два фермиона (частицы с полуцелым спином, такие как электроны) не могут находиться в одном и том же квантовом состоянии одновременно. Это свойство объясняет структуру атомов и, в частности, то, как электроны распределяются по энергетическим уровням в атомах. Благодаря этому принципу образуются химические связи, что, в свою очередь, определяет свойства веществ.
Спин электрона также имеет важное значение в области квантовой информации и квантовых вычислений. Квантовые биты (кубиты), использующие спин электрона, могут находиться в состоянии суперпозиции, что позволяет осуществлять вычисления с высокой степенью параллелизма. Это открывает новые горизонты для разработки квантовых компьютеров, которые могут решать задачи, недоступные классическим вычислительным системам.
Наконец, спин электрона связан с явлением спиновой поляризации, которое наблюдается в различных материалах. Спиновые поляризованные электроны могут влиять на проводимость и другие физические свойства материалов, что имеет важное значение для разработки новых технологий, таких как спинтроника. Спинтроника использует спин электрона для хранения и обработки информации, что может привести к созданию более быстрых и эффективных электронных устройств.
Вопрос-ответ
Что такое спин простым языком?
Спин (от англ. Spin – вращаться) – собственный момент количества движения элементарной частицы, имеющий квантовую природу и не связанный с её перемещением в пространстве как целого.
Что значит спин 2?
Спин-2 является квантово-механическим свойством, указывающим на внутренний угловой момент частицы, равный двум единицам Планка. Это особенность, которая делает частицы со спином-2 уникальными в мире элементарных частиц, в том числе гипотетические гравитоны, предполагаемые переносчики гравитационного взаимодействия.
Советы
СОВЕТ №1
Изучите основные принципы квантовой механики, чтобы лучше понять концепцию спина электрона. Спин является одной из ключевых характеристик частиц, и знание основ квантовой механики поможет вам осознать, как он влияет на поведение электронов.
СОВЕТ №2
Обратите внимание на эксперименты, связанные со спином, такие как эксперимент с двойной щелью и магнитные свойства материалов. Это поможет вам увидеть, как спин электрона проявляется в реальных физических явлениях и технологиях.
СОВЕТ №3
Используйте визуальные материалы, такие как диаграммы и анимации, чтобы лучше представить себе концепцию спина. Визуализация может значительно облегчить понимание абстрактных понятий, связанных с квантовой физикой.
СОВЕТ №4
Обсуждайте тему спина с другими заинтересованными людьми или в учебных группах. Обсуждение и обмен мнениями могут помочь вам глубже понять материал и увидеть его с разных точек зрения.








